Allometries and conversions
Lauren Buckley and the TrEnCh project, Department of Biology, University of Washington
2023-09-29
Source:vignettes/AllometryAndConversionsTutorial.Rmd
AllometryAndConversionsTutorial.RmdThis tutorial reviews tools that use allometries to estimate the dimensions of organisms needed for energy balances and other analyses. The tutorial also documents convenience functions for converting units. Finally, we present functions that describe thermal performance curves.
Allometries
We provide tools for estimating additional dimensions of organisms from measured dimensions.
Mass
The function mass_from_length() encompasses
empirically-derived relationships to estimate mass as a power law
function of mass for six taxonomic classifications. The relationships
are derived by relating length to mass for specimens of numerous
species. We use the mass_from_length() function to
illustrate the allometries for different taxa:
oldpar<- par()
par(mar = c(5, 5, 2, 2))
plot(x = seq(0.01, 0.25, 0.01),
y = mass_from_length(l = seq(0.01, 0.25, 0.01),
taxon = "lizard"),
type = "l",
xlab = "length (m)",
ylab = "mass (g)",
ylim = c(0, 200),
xlim = c(0, 0.25),
las = 1,
bty = "L",
lwd = 2)
points(x = seq(0.01, 0.25, 0.01),
y = mass_from_length(l = seq(0.01, 0.25, 0.01),
taxon = "salamander"),
type = "l",
col = "blue",
lwd = 2)
points(x = seq(0.01, 0.25, 0.01),
y = mass_from_length(l = seq(0.01, 0.25, 0.01),
taxon = "frog"),
type = "l",
col = "red",
lwd = 2)
points(x = seq(0.01, 0.25, 0.01),
y = mass_from_length(l = seq(0.01, 0.25, 0.01),
taxon = "snake"),
type = "l",
col = "green",
lwd = 2)
points(x = seq(0.01, 0.25, 0.01),
y = mass_from_length(l = seq(0.01, 0.25, 0.01),
taxon = "turtle"),
type = "l",
col = "orange",
lwd = 2)
points(x = seq(0.01, 0.25, 0.01),
y = mass_from_length(l = seq(0.01, 0.25, 0.01),
taxon = "insect"),
type = "l",
col = "purple",
lwd = 2)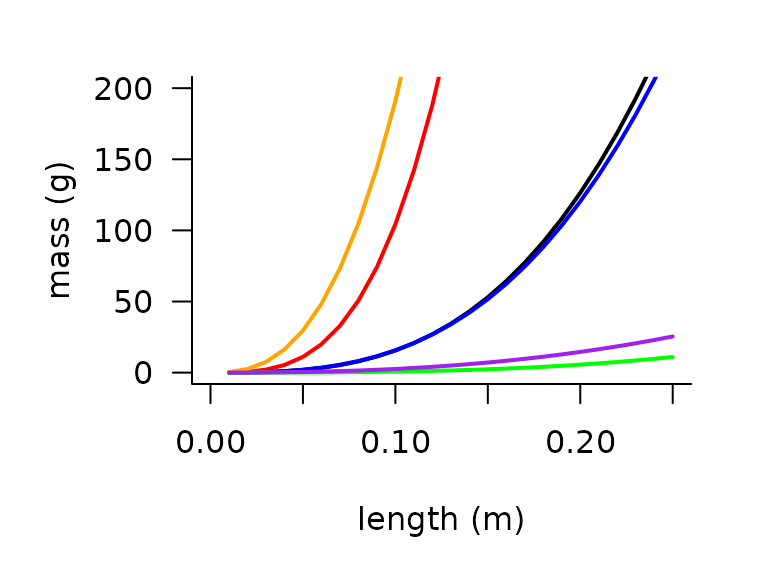
Surface Area
Surface area is needed for several aspects of biophysical models but is rarely measured. We provide functions to estimate surface area (\(m^3\)) from length, mass, or volume for a variety of taxa.
The function surface_area_from_mass() encompasses
empirically-derived relationship to estimate surface area as a power law
function of mass for lizards, frogs, and insects.
par(mar = c(5, 5, 2, 2))
plot(x = 1:50,
y = surface_area_from_mass(m = 1:50,
taxon = "lizard"),
type = "l",
xlab = "mass (g)",
ylab = "",
las = 1,
bty = "L",
lwd = 2)
mtext(text = expression("surface area" ~ (m^{2})),
side = 2,
line = 3.5)
points(x = 1:50,
y = surface_area_from_mass(m = 1:50,
taxon = "frog"),
type = "l",
lty = "dashed",
lwd = 2)
points(x = 1:50,
y = surface_area_from_mass(m = 1:50,
taxon = "salamander"),
type = "l",
lty = "dotted",
lwd = 2)
points(x = seq(0.1, 5, 0.2),
y = surface_area_from_mass(m = seq(0.1,5,0.2),
taxon = "insect"),
type = "l",
lty = "dotdash",
lwd = 2)
box(bty = "L",
lwd = 2)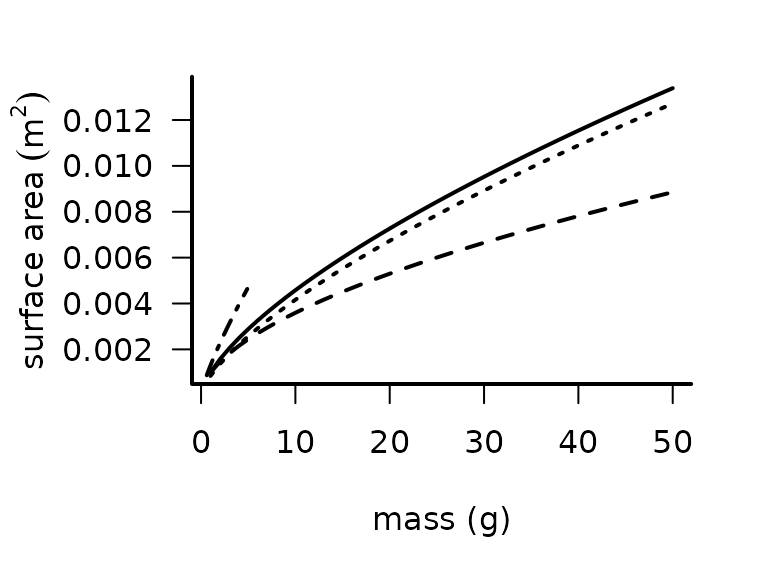
We also provide empirical relationships estimating surface area as power law function of volume. The functions were developed by Mitchell (1976) for use in approximating convective heat transfer:
plot(x = seq(0.001, 0.01, 0.001),
y = surface_area_from_volume(V = seq(0.001, 0.01, 0.001),
taxon = "lizard"),
type = "l",
xlab = expression(volume ~ (m^{3})),
ylab = expression("surface area" ~ (m^{2})))
points(x = seq(0.001, 0.01, 0.001),
y = surface_area_from_volume(V = seq(0.001, 0.01, 0.001),
taxon = "frog"),
type = "l",
lty = "dashed")
points(x = seq(0.001, 0.01, 0.001),
y = surface_area_from_volume(V = seq(0.001, 0.01, 0.001),
taxon = "sphere"),
type = "l",
lty = "dotted")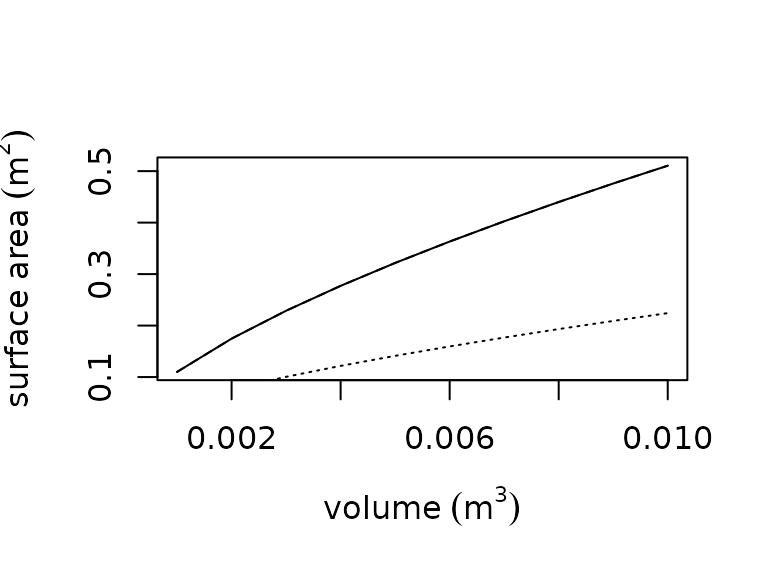
For the same study, we additionally provide a function to estimate volume from length for several taxa or by approximating the organism as a sphere. Finally, we provide a function for estimating surface area from length by approximating the animal’s body as a rotational ellipsoid. The allometric functions are available in R as follows:
par(mar = c(5, 5, 2, 2))
plot(x = seq(0.01, 0.05, 0.001),
y = volume_from_length(l = seq(0.01, 0.05, 0.001),
taxon = "lizard"),
type = "l",
xlab = "length (m)",
ylab = expression(volume ~ (m^{3})))
points(x = seq(0.01, 0.05, 0.001),
y = volume_from_length(l = seq(0.01, 0.05, 0.001),
taxon = "frog"),
type = "l",
lty = "dashed")
points(x = seq(0.01, 0.05, 0.001),
y = volume_from_length(l = seq(0.01, 0.05, 0.001),
taxon = "sphere"),
type = "l",
lty = "dotted")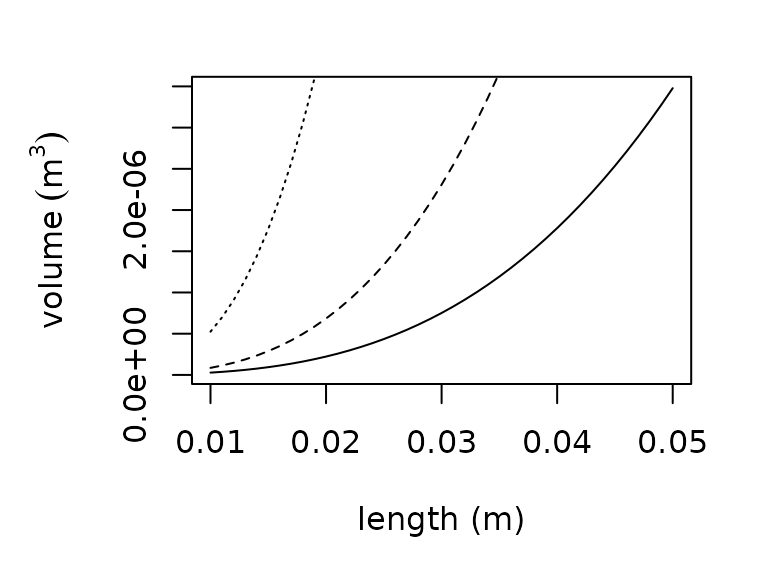
par(mar = c(5, 5, 2, 2))
plot(x = seq(0.01, 0.05, 0.001),
y = surface_area_from_length(l = seq(0.01, 0.05, 0.001)),
type = "l",
xlab = "length (m)",
ylab = expression("surface area" ~ (m^{2})))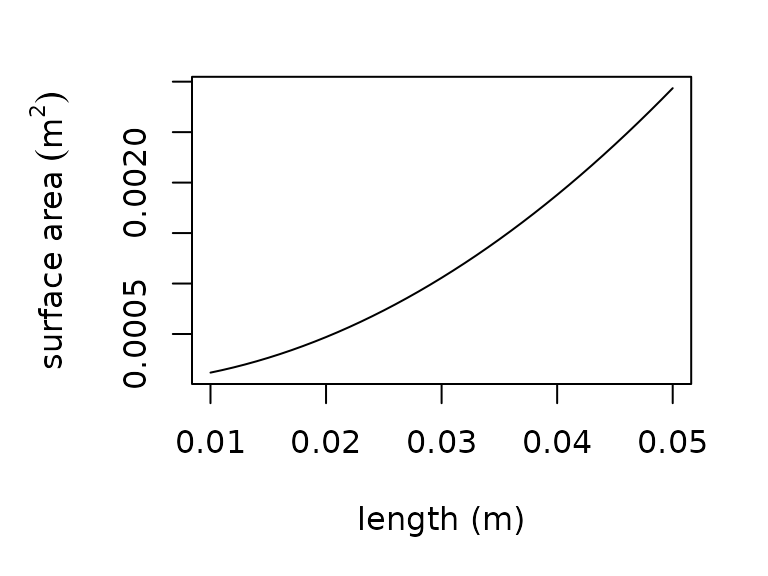
Estimating the amount of solar radiation that an animal absorbs
requires knowledge of the silhouette area, the proportion of an animal’s
surface area that is projected onto a horizontal surface. Silhouette
area is a function of the sun’s angle. We offer empirically-derived
relationships to predict the proportional silhouette area for frogs,
lizards, and grasshoppers as a polynomial function of zenith angle
(proportion_silhouette_area()). We additionally offer a
function (proportion_silhouette_area_shapes()) to estimate
silhouette area by approximating the animal as a sphere or cylinder as a
function of theta, the angle between the solar beam and the longitudinal
axis. The R functions are parameterized as follows:
par(mar = c(5, 5, 2, 2))
plot(x = seq(0, 90, 10),
y = proportion_silhouette_area(psi = seq(0, 90, 10),
taxon = "frog"),
type = "l",
xlab = "zenith angle (°)",
ylab = "proportion silhouette area",
ylim = range(0, 0.5))
points(x = seq(0, 90, 10),
y = proportion_silhouette_area(psi = seq(0, 90, 10),
taxon = "lizard",
raz = 0,
posture = "prostrate"),
type = "l",
lty = "dashed")
points(x = seq(0, 90, 10),
y = proportion_silhouette_area(psi = seq(0, 90, 10),
taxon = "lizard",
raz = 0,
posture = "elevated"),
type = "l",
lty = "dotted")
points(x = seq(0, 90, 10),
y = proportion_silhouette_area(psi = seq(0, 90, 10),
taxon = "grasshopper"),
type = "l",
lty = "dotdash")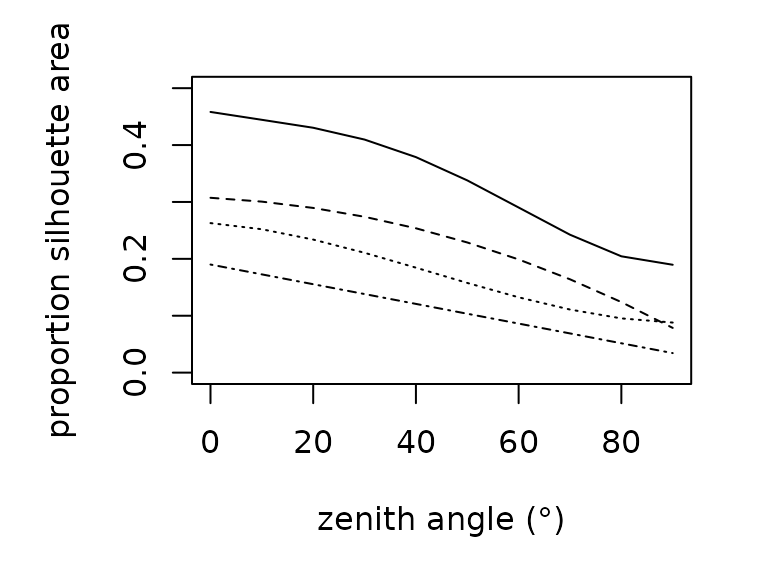
plot(x = seq(0, 90, 10),
y = proportion_silhouette_area_shapes(shape = "spheroid",
theta = seq(0, 90, 10),
h = 0.4,
d = 0.39),
type = "l",
xlab = "theta (°)",
ylab = "proportion silhouette area",
ylim = c(0, 0.35),
lty = "dashed")
points(x = seq(0, 90, 10),
y = proportion_silhouette_area_shapes(shape = "spheroid",
theta = seq(0, 90, 10),
h = 0.4,
d = 0.3),
type = "l",
lty = "dashed")
points(x = seq(0, 90, 10),
y = proportion_silhouette_area_shapes(shape = "spheroid",
theta = seq(0, 90, 10),
h = 0.4,
d = 0.2),
type = "l",
lty = "dotted")
points(x = seq(0, 90, 10),
y = proportion_silhouette_area_shapes(shape = "spheroid",
theta = seq(0, 90, 10),
h = 0.4,
d = 0.1),
type = "l",
lty = "dotdash")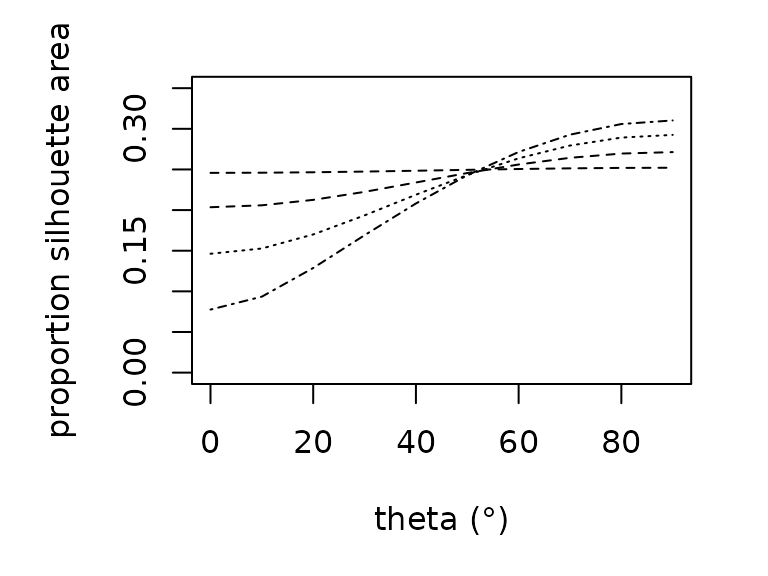
plot(x = seq(0, 90, 10),
y = proportion_silhouette_area_shapes(shape = "cylinder flat ends",
theta = seq(0, 90, 10),
h = 0.4,
d = 0.4),
type = "l",
lty = "dashed",
xlab = "theta (°)",
ylab = "proportion silhouette area",
ylim = c(0, 0.35))
points(x = seq(0, 90, 10),
y = proportion_silhouette_area_shapes(shape = "cylinder flat ends",
theta = seq(0, 90, 10),
h = 0.4,
d = 0.2),
type = "l",
lty = "dashed")
points(x = seq(0, 90, 10),
y = proportion_silhouette_area_shapes(shape = "cylinder flat ends",
theta = seq(0, 90, 10),
h = 0.4,
d = 0.1),
type = "l",
lty = "dotted")
points(x = seq(0, 90, 10),
y = proportion_silhouette_area_shapes(shape = "cylinder flat ends",
theta = seq(0, 90, 10),
h = 0.4,
d = 0.05),
type = "l",
lty = "dotdash")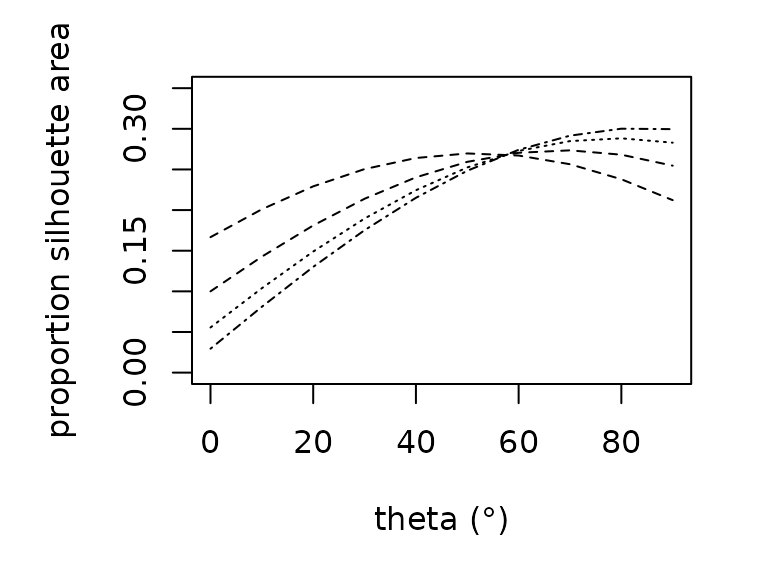
plot(x = seq(0, 90, 10),
y = proportion_silhouette_area_shapes(shape = "cylinder hemisphere ends",
theta = seq(0, 90, 10),
h = 0.4,
d = 0.4),
type = "l",
xlab = "theta (°)",
ylab = "proportion silhouette area",
ylim = c(0, 0.35))
points(x = seq(0, 90, 10),
y = proportion_silhouette_area_shapes(shape = "cylinder hemisphere ends",
theta = seq(0, 90, 10),
h = 0.4,
d = 0.2),
type = "l",
lty = "dashed")
points(x = seq(0, 90, 10),
y = proportion_silhouette_area_shapes(shape = "cylinder hemisphere ends",
theta = seq(0, 90, 10),
h = 0.4,
d = 0.1),
type = "l",
lty = "dotted")
points(x = seq(0, 90, 10),
y = proportion_silhouette_area_shapes(shape = "cylinder hemisphere ends",
theta = seq(0, 90, 10),
h = 0.4,
d = 0.05),
type = "l",
lty = "dotdash")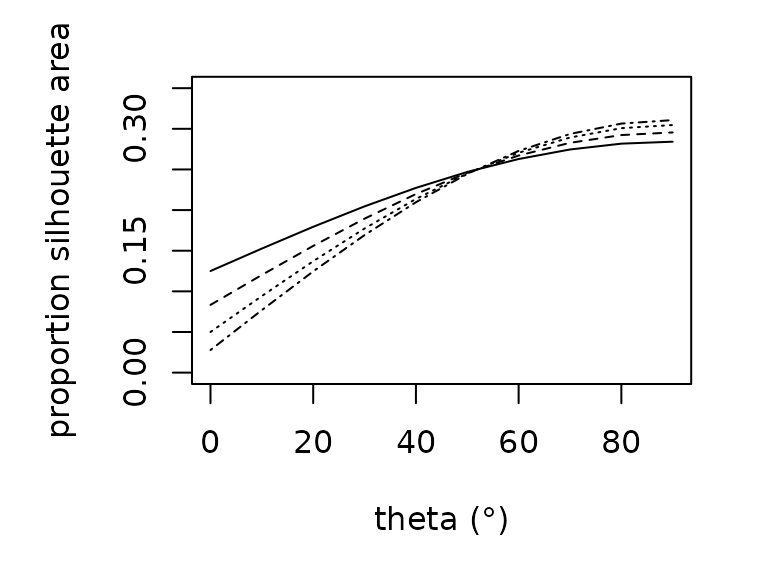
Conversions
We offer convenience functions to convert among units for angles and temperatures:
degrees_to_radians(47.608)## [1] 0.8309164
radians_to_degrees(0.831)## [1] 47.61279## [1] 29.44444## [1] 302.5944
kelvin_to_celsius(270)## [1] -3.15Thermal Performance Curve Functions
Thermal performance curves (TPCs) describe the temperature dependence
of organismal performance such as locomotion and digestion (Huey and Kingsolver 1989). They have become an
important tool to understand organismal responses to environmental
conditions, particularly responses to climate change (Sinclair et al. 2016). TrenchR includes two
forms of TPCs. We include a function TPC() to describe a
Gaussian-quadratic TPC as a function of thermal optima and critical
thermal minima and maxima (Deutsch et al.
2008). The TPC_beta() function uses a beta function
to define a TPC based on mode, breadth, and skew. A scale factor enables
including a thermodynamic effect on mean performance (Asbury and Angilletta Jr 2010). Additional TPC
resources are available in the R packages rTPC and thermPref.
plot(x = 0:60,
y = TPC(T = 0:60,
T_opt = 30,
CT_min = 10,
CT_max = 40),
type = "l",
ylim = c(0,3),
ylab = "performance",
xlab = "temperature (°C)")
points(x = 0:60,
y = TPC_beta(T = 0:60,
shift = -1,
breadth = 0.1,
aran = 0,
tolerance = 43,
skew = 0.7),
type = "l",
lty = "dashed")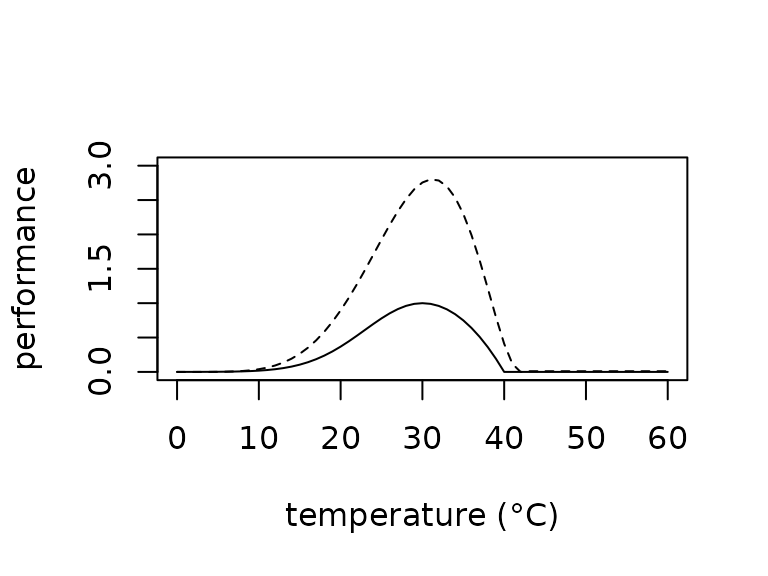
suppressWarnings(par(oldpar))